那今天,我打算一步一步寫出演算法,順便跟大家分享關於我的理解,首先決策樹算法有ID3和C4.5和CART算法,今天要講解的是CART分類法(因為此方法既可以做分類也可以做回歸兩種都可以,其他方法只能做分類):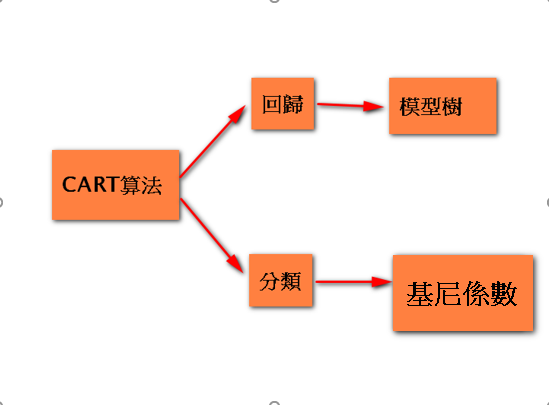

首先今天要介紹CART算法中的分類,首先是基尼不純度, 基尼不純度表示一個隨機選中的樣本在子集中被分錯的可能性。基尼不純度為這個樣本被選中的概率乘以它被分錯的概率。當一個節點中所有樣本都是一個類時，基尼不純度為零。公式如下: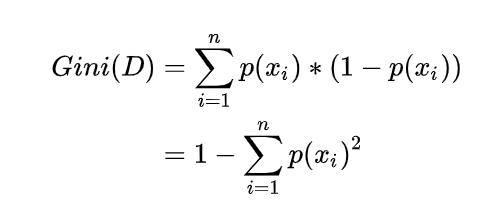

D表示數據集(總共有1,2…,n種分類,分別是x_1,x_2 〖,…,x〗_n),P(x_i)表示被標記成x_i類的機率值(也就是數據分類到i)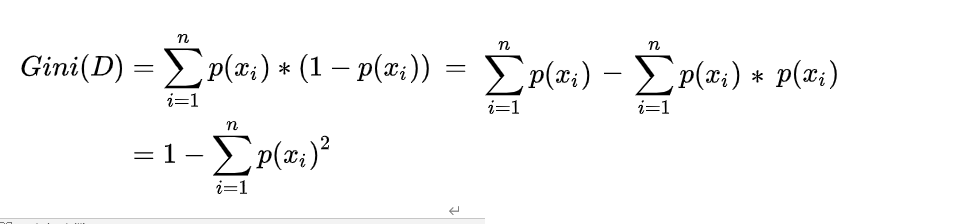

而通常P(x_i)為: 該組資料個數/全部資料個數
所以最後,如果把它寫成程式碼就會像這樣:
假設資料被分類成1,2類(第0維為y)後面為其餘特徵

data=[[1,"a",0.852],[2,"b",0.31],[1,"b",0.589],[1,"c",0.01],[2,"c",0.258]]

然後我們定義基尼不純度的函數:

import random as rd
def Gini_imp(data):
    #首先創建一個字典計算指標個數
    dict_label = {}
    for i in data:
        right_Label = i[0]
        dict_label[right_Label] = dict_label.get(right_Label, 0) + 1
    print(dict_label)
    #一開始機率值1
    Gini_pro = 1
    #依照公式1-sum(pi**2) 和 pi為 第i類資料個數/全部資料個數
    for key in dict_label:
        pi = dict_label[key] / len(data)
        Gini_pro -= pi * pi
    return Gini_pro
   

然後我們把資料帶入

data=[[1,"a",0.852],[2,"b",0.31],[1,"b",0.589],[1,"c",0.01],[2,"c",0.258]]
print(Gini_imp(data))

類1有3個,類2有2個
1-(3/5)^2-(2/5)^2=1-(9/25)-(4/25)=(12/25)=0.48
顯示結果就會如下:

{1: 3, 2: 2}
0.48

再來對於樣本D,根據某一條件con(後面會在說明)，把樣本D分成兩部分D1和D2
公式如下:
而|D|為D總共樣本個數, D1和D2以此類推:
所以程式如下:
把資料分割成D1和D2

data1=[[1,"a",0.852],[2,"b",0.31],[1,"b",0.589]]
print(Gini_imp(data1))

data1的基尼不純度為: 0.44

data2=[[1,"c",0.01],[2,"c",0.258]]
print(Gini_imp(data2))

data2的基尼不純度為: 0.5
然後下面計算D的基尼係數
Gini_D=(3/5)X0.44+(2/5)X0.5 = 0.4666
程式如下:

#data(第0維為y)
data=[[1,"a",0.852],[2,"b",0.31],[1,"b",0.589],[1,"c",0.01],[2,"c",0.258]]
data1=[[1,"a",0.852],[2,"b",0.31],[1,"b",0.589]]
data2=[[1,"c",0.01],[2,"c",0.258]]
def Gini_cofe(data1,data2):
    Gini_1 = len(data1)* Gini_imp(data1) / (len(data1)+len(data2))
    Gini_2 = len(data2)* Gini_imp(data2) / (len(data1)+len(data2))
    Gini_c = Gini_1 + Gini_2
    return Gini_c
print(Gini_cofe(data1,data2))

0.46666

好,今天實作部分就到這,明天再開始說明資料袋裝抽樣
以上程式和之後隨機森林都參考這篇https://codertw.com/%E7%A8%8B%E5%BC%8F%E8%AA%9E%E8%A8%80/466826/

在男孩前往森林的路上時,一朵木棉花從天空飄來下來,降在男孩身後,男孩沒有察覺,繼續地往前走去,花降落地上後,瞬間腐爛,裡面有一隻蒼蠅飛了出來, 奇怪的是,蒼蠅飛舞並未發出任何聲音,蒼蠅並未往男孩飛去,而是朝著男孩離開的木屋飛去 				
                  --|從未結束,一切只是開始|--     CS.MM